计算机扫盲贴|第二章_比特、字节与信息表示

        这一章，我们来讨论计算机表示信息的三个基本思想。
        
        首先，计算机是数字处理器。它们存储和处理离散的信息，这些信息表现为不连续的块，具有不连续的值，基本上就是一个个数值。而与之相对的模拟信息，则是平滑变化的值。

        其次，计算机用比特表示信息。比特就是二进制数字，即一个非0即1的值。计算机中的一切都用比特来表示。计算机内部使用二进制，而不是人们所熟悉的十进制。
🤞🌧🥩♾🦌‏        
        再次，较大的信息以比特组表示。数值、字母、单词、姓名、声音、照片、电影，以及处理这些信息的程序所包含的指令，都是用比特组来表示的。
        
        本章关于数字的讨论并不是非看不可，但其背后的思想却非常重要。
        
🤌🌡🦞✡🦕‎        2.1模拟与数字
        
        首先，我们谈一谈模拟与数字的区别。“模拟”（analog)与“类似的”（analogous)词根相同，表达的意思是：值随着其他因素变化而平滑变化。现实生活中的很多事物都具有模拟性质，比如水龙头或汽车方向盘。如果你想让车转个小弯，轻轻打一打方向盘即可，打多打少由你自己来定。拿它跟转向灯作个比较，后者要么开要么关，没有中间状态。在模拟装置中，某些事物（汽车转弯幅度）会随另一些事物（方向盘转动幅度）的变化平滑而连续地变化。变化过程没有间断，一个事物的微小变化就意味着另一个事物的微小变化。
        
        数字系统处理的是离散值：可能的取值是有限的（转向灯只可能是关闭的或在左右方向打开)。某个事物小小的变化，要么不引发其他事物变化，要么就引发其他事物的突变，使其从一个离散的值跳到另一个离散的值。👨‍🎨‏💎🏮🤬🙌
        
        比如手表。“模拟”手表有时针、分针和秒针，秒针每分钟转一圈。虽然现代的手表都由内部的数字电路控制，但时针和分针仍然随着时间流逝而平滑移动，而且三根表针都能走遍所有可能的位置。数字手表或手机时钟显示的时间只有数值。显示屏每秒变化一次，每分钟更新一次分钟的值，但不会显示分钟的小数位。
        
        再比如汽车的速度表。大多数汽车都有模拟速度表，速度指针平滑地上下移动，按比例指示汽车的速度。从一个速度到另一个速度的过渡是平滑的，没有间断。与之相对，汽车的GPS导航仪则用数字来显示最接近的时速，不管单位是英里/小时还是公里/小时。稍微加点速，速度值会从65变成66,再减点速就又变回65，但永远不会出现65.5。
        ‏👠💿😂
        又比如温度计。温度计的红色液体（通常是染色酒精）或水银柱是模拟的：液体会随着温度变化按比例膨胀或收缩，因此温度产生较小的变化，液体柱高度也会相应产生较小变化。但大楼外面显示温度的广告牌则是数字的：显示屏显示的是数值，温度介于36.5和37.4之间时，它都显示为37。
        
        这可能会导致一些奇怪的情况。几年前，我在美国高速公路上开车，收听到加拿大电台的节目。加拿大采用公制单位，播音员出于好意，想照顾到所有美加的听众，就如此宣布说：“刚才的一小时，华氏度上升了一度，摄氏度没有变化。
        
        有人要问，为什么用数字而不用模拟呢？我们这个世界可是模拟的呀，而且手表、速度表等等模拟设备也更容易让人一目了然。但不管怎样，很多现代的技术都是数字的，而且我们这本书也是在讲述数字的故事。

👨‍🎨‎🦺🧬🤬👌

        外部世界的数据——声音、图片、运动、温度，等等一切，在输人端都会尽可能早地转换为数字形式，而在输出端则会尽可能晚地转换回模拟形式。原因就在于数字化的数据容易处理，无论最初来源是什么，数字化数据都可以用多种方式来存储、传输和处理，但模拟信息则不行。

        第9章将会介绍，通过删除冗余和不重要的信息，还可以压缩数字化信息。为了安全和隐私可以对它进行加密，可以将它与其他数据合并，可以复制它而不出错，可以通过互联网把它发送到任何地方，可以将它保存到几乎无限种设备中。而对于模拟信息，上述很多做法是根本行不通的。
        
✍🏝🥭🆎🐻‎        与模拟系统相比，数字系统还有另一个优势，就是它更容易扩展。

        比如说，给模拟天文馆增加一颗新发现的星星，专业人员必须辛苦地做出光照效果来；而在数字天文馆，只要在数据文件里添加一行信息即可。我的数字手表可以连续不断地以百分之一秒显示时间流逝，而要让模拟手表做到这一点可就太难了。不过，模拟系统有时候也有它的优势，像泥版、石雕、羊皮纸、图书和照片等古老的媒体，都经历了数字格式未曾经历过的时间考验。
        
        2.2模数转换
💅🧳🍧☯🐢‍        
        怎么把模拟信息转换为数字形式？我们还是举几个简单的例子吧，先说照片和音乐，通过它们可以说明一些重要的思想。
        
        把照片转换为数字形式，应该是最容易想象的了。假设我们给自家的小猫拍张照片：

🧑‍⚕️‎🛍📮😄🖕

        胶卷相机的成像，是通过把胶片感光区曝露给被拍物体反射的光线实现的，胶片上不同区域接收到的不同颜色的光量不同，从而影响胶片上的染料。在胶片显影、印相时，彩色染料数量决定了显示出来的颜色变化。
        
        对数码相机来说，镜头把影像聚焦到一块位于红、绿、蓝滤镜后面的矩形感光器阵列上，感光器由微小的光敏探测器组成。每个探测器存储一定数量的电荷，与落在它上面的光量成正比。这些电荷被转换为数字值，照片的数字表示就是这些表现光强度的数值序列。探测器越小，数量越多，电荷测量的结果就越精细，数字化图像就能越精确地反映原始的影像。
        👮‍♂️‌💎📬👻🤛
        传感器阵列的每个单元都由一组能够捕获红、绿、蓝光的探测器构成，每个单元对应一个像素，即像元。3000x2000像素的图像，包含600万个像元，或600万像素，对今天的数码相机而言并不算大。像素的颜色通常由三个值表示，分别代表红、绿、蓝光的强度，因此600万像素的图像总共要存储1800万个颜色值。屏幕在显示图像时，使用的是红、绿、蓝光三元组的阵列，其亮度与像素亮度一致。如果你用放大镜仔细观察手机或电脑屏幕，很容易看到每个独立的彩色块。
        
        第二个模数转换的例子是声音，尤其是音乐。之所以说音乐是个不错的例子，原因在于以它为代表的数字信息的所有权，第一次引起了社会、经济和法律上的广泛关注。

        数字音乐与唱片或磁带不同，你可以在自己家的计算机里无限次地复制它，完全免费，而且还可以通过互联网把它复制发送到世界的任何角落，不会有任何音质损失，同样完全免费。唱片业把这当成了严重的威胁，试图通过法律或政治手段阻止数字音乐的拷贝。这场战争远未结束，每天都有小规模的战役打响，因此而对簿公堂和引爆政治辩论俨然成了家常便饭。

🦴🦼🫖❎🪶‏

        
        什么是声音？音源通过振动或快速运动引起空气压力的波动，人的耳朵把这种压力变化转换为神经活动，经大脑解释之后就形成了“声音”。1870年代，托马斯·爱迪生制造了一个叫做“留声机”的机器，这台机器能把声波转换为蜡筒上类似的螺旋沟槽，而通过这些沟槽又能再次创造出同样的气压波动来。把声音转换为沟槽就是“录音”，而从沟槽换回到气压波动就是“回放”。

        爱迪生的发明迅速地得到改进，1940年代就出现了密纹唱片（long-playing record)或简称LP,而且至今还在使用（尽管数量已经不多了）。麦克风随着时间推移把变化的声压转换为变化的值并记录下来，然后根据这些值在乙烯基的盘片上压制出与声压一致的螺旋沟槽。播放LP时，唱针随着沟槽起伏，其运动轨迹被转换为波动的电流，电流经过放大后驱动扬声器或耳机，通过它们的振动薄膜产生声音。
👩‏👠🪥😷🤙

        把空气压力随时间的变化形象地绘制出来并不难。其中压力可以用任何物理方法来表示，在此我们假设用电路中的电压。当然，电流、光的亮度，以及爱迪生发明的留声机中的纯机制装置都没有问题。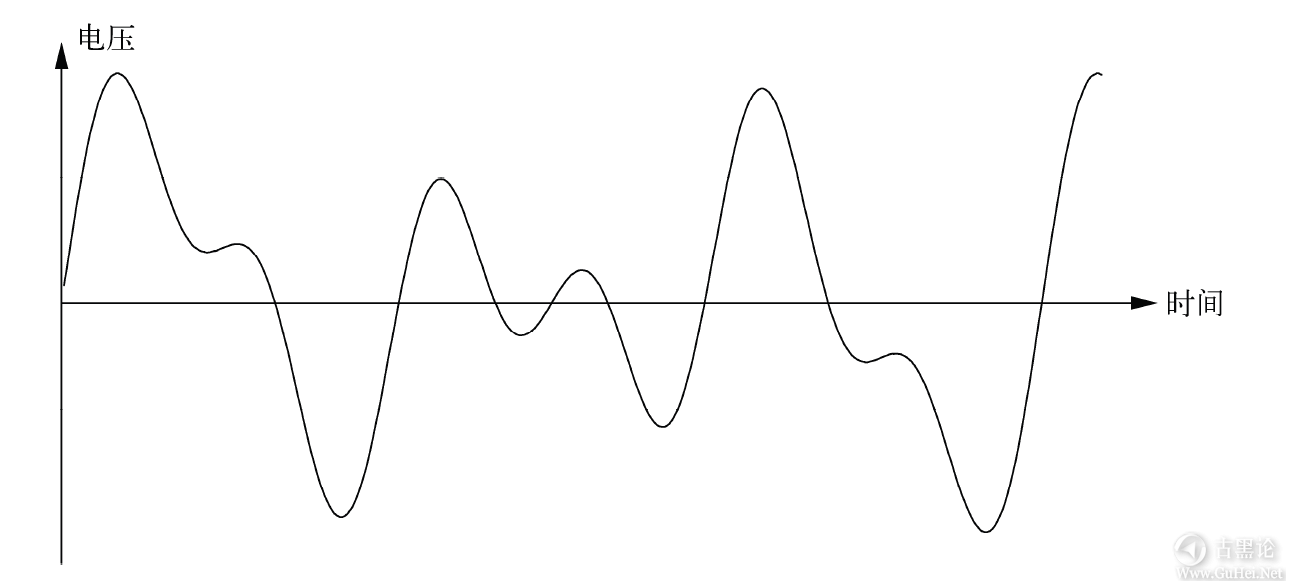


        图中声波的高度表示声音强度或大小，水平方向的坐标轴表示时间：每秒钟声波的数量就是声调或频率。假设我们以固定时间间隔连续测量这条曲线的高度（在这里就是电压值），就会得到下图所示的这些垂直线条。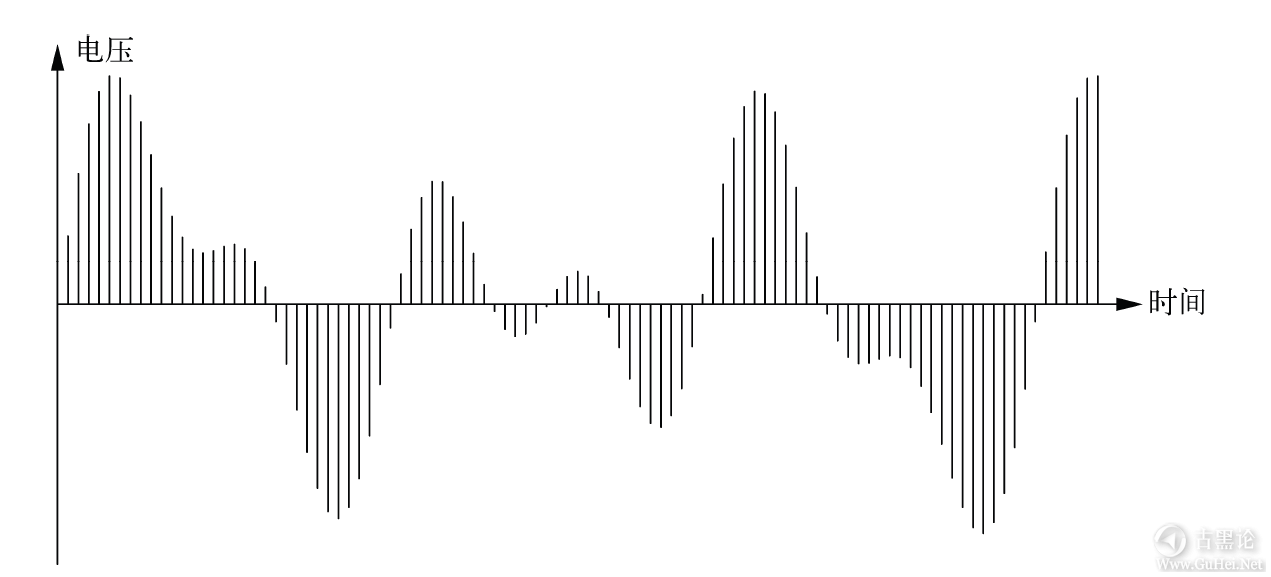
🤛🏦🍼⁉🐅‌

        测量得到的数值连接起来与曲线近似，测量越频繁，越准确，结果也就越吻合。测量得到的数值序列是波形的数字化表示，可以存储、复制、操作它们，也可以把它们发送到任何地方。如果有设备把这些数值转换成对应的电压或电流，然后再通过电压或电流驱动音箱或耳机，就能够实现回放。从声波到数值是模数转换，相应的设备叫A/D转换器；反过来当然是数模转换，或者叫D/A。转换过程并不是完美无缺的，两个方向的转换都会损失一点信息。但大多数情况下，这种损失是人所觉察不到的（当然，也有不少唱片发烧友会说CD音质不如LP好)。
        
        1982年左右，音频光盘（或CD)面世，成为最早承载数字声音的产品。今天的小伙伴们，恐怕没有谁不认识这个标志：🧑‍🌾‎🧢📡😍🤳


        与LP唱片上的模拟沟槽不同，CD用长长的螺旋状轨道在盘面的一侧记录数值。轨道上任意一个区块的表面要么平滑，要么是一个微小的凹坑。这些下凹或平滑的区块就是用来编码声波的数字值的，每个区块是一位，连续的多位表示二进制编码中的一个数值，二进制的概念我们在下一节再介绍。

        光盘旋转时，一束激光照射到轨道上，而光电传感器则检测每个区块上反射回来的光量多少。如果光量不多，说明是凹坑；如果反射光很强，说明不是凹坑。标准CD编码采样率为每秒44100次，而每次采样获得两个振幅值（立体声的左、右声道），精确度为65536(即216，这并非巧合）分之一。轨道上的每个区块非常非常小，小到只有用显微镜才能看见，一张CD的表面上有60亿个小区块。（DVD中的区块更小，由于区块更小，激光束频率更高，DVD的存储容量近5GB，而CD大约为700MB。）🧒‎🪖⌨😇🖐
        
        音频CD的出现几乎让LP没有了立足之地，相比之下，CD的优点实在太多了：落上点灰尘也不用太担心了，更没有磨损一说，而且绝对小巧。但到了我写这本书的时候，LP开始在某种程度上复苏，流行音乐CD的人气则日渐衰退。有朝一日，CD很可能也会像LP—样变成古董，这倒让我很高兴，因为我收藏的音乐全部都是CD格式的。我现在完全拥有它们，而它们的存在将比我的生命更久远。CD还有第二个用途，那就是作为存储、分发软件及数据的介质，不过这个功能已经被DVD取代，而DVD很可能又会被下载所取代。
        
        声音和图片经常会被压缩，因为这两种媒体包含很多人类根本感知不到的细节。对于音乐，典型的压缩技术是MP3,大约能把音频文件的体积压缩到原来的十分之一，同时几乎让人感觉不到音质下降。对于图片，最常用的压缩技术是JPEG(是制定该标准的联合图像专家组——Joint Photographic Expert Group的英文字头），它的压缩率也能达到10倍甚至更高。上文提到很多处理对数字信息能做，但对模拟信息却很难（或不可能），压缩就是一个例子。第9章我们再进一步探讨压缩。
        
👂🛑🍍♏🐢‏        那电影呢？1870年代，摄影师埃德沃德·迈布里奇向世人证明，快速连续地显示一系列静态图片能够创造出运动的错觉。今天，电影显示影像的速度是每秒24帧，而电视大约是25到30帧，这个速度足以让人的眼睛把顺序播放的影像感知为动画。而通过组合（并同步）声音和影像，就可以创造出数字电影。

        而利用压缩技术减少空间占用，则催生了包括MPEG(代表Moving Picture Experts Group)在内的标准电影格式。实际上，视频的表示要比单纯的音频表示更复杂，一方面是它本身就复杂，另一方面很大程度上还因为它受到了电视的拖累，而电视在其存在的大部分时间内都是模拟的。模拟电视在世界范围内正逐渐被淘汰，而美国2009年已经将广播电视切换成了数字信号。
        
        还有一些信息很方便以数字形式来表示，因为除了想好如何表示它之外，根本不需要做什么转换。比如这本书中的文字、字母、数字和标点符号，我们称为其普通文本。可以为其中每个字母指定一个唯一的数值，如A是1，B是2等等，这不就是一种数字化表示方法嘛。而事实也正是如此，只不过在表示标准中，A到Z用的是65到90,a到z用的是97到122,数字0到9用的是48到57,而标点符号等其他字符用的是其他数值。这个表示标准叫做ASCII，即American Standard Codefor Information Interchange(美国信息交换标准代码)。👩‍✈️‍🎩📞😒✌
        
        下面给出了ASCII中的部分标准编码，前四行被我省略了，因为其中包含的都是些制表符、空格符等非打印字符。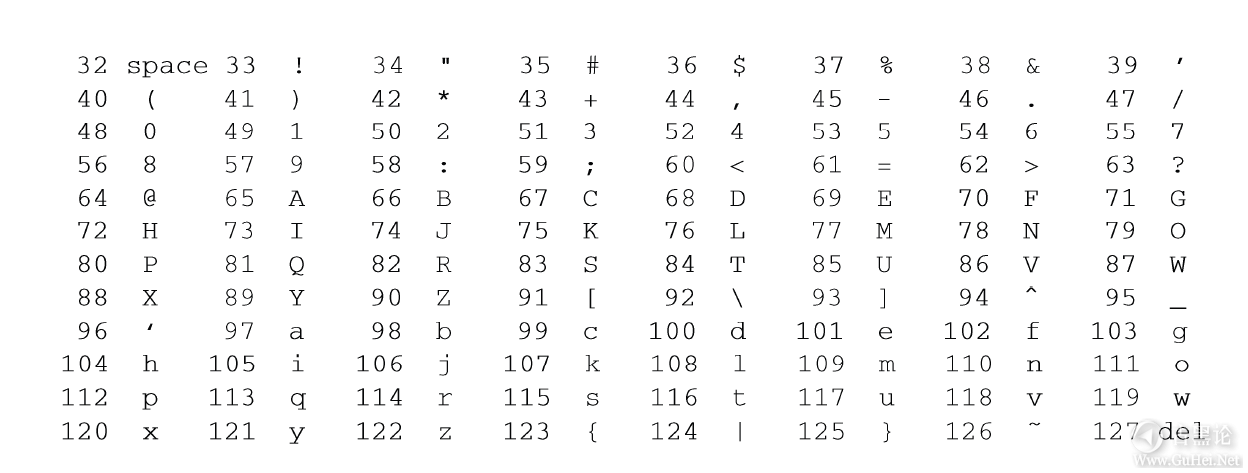


        不同地区有不同的字符集标准，但也有一个世界通用的标准叫Unicode，它为所有语言的所有字符都规定了一个唯一的数值。这是一个非常庞大的字符集，人类的创造力是无穷无尽的，但在建立自身书写系统方面却很少有规则。目前，Unicode涵盖的字符远远超过100000个，而且这个数字还在稳步增长。可想而知，Unicode中的大部分都是包括中文在内的亚洲字符集，但决不限于此。要了解Unicode都包含哪些字符集，可以访问unicode.org，这个站点内容丰富，强烈推荐小伙伴们去看一看。👩‎🎒🪦😛🤛
        
        一言以蔽之：数字表示法能够表示上述所有信息，以及任何可以转换为数值的信息。因为只有数值，所以就可以用数字计算机来处理，而且正如第9章要介绍的，还可以通过互联网等通用数字网络将它复制到其他计算机上去。
        
        2.3比特、字节与二进制
        

👨🦱‍📀😒🤟

        “世界上只有10种人，理解二进制的和不理解二进制的。”数字系统用数值来表示所有信息，但使用的却不是我们熟悉的（以10为基数的）十进制，这乍一看让人有点纳闷。那使用几进制？使用二进制，也就是逢2进1的数制。
        
        虽说是人都或多或少懂点数学，但以我的经验来看，人们对数值的理解有时候并不靠谱。这一点从描述（再熟悉不过的）十进制和（多数人不熟悉的）二进制之间的关系就可以看出来。在这一节里，我会尽最大努力讲得通俗易懂，万一你听不懂或者我没讲清楚，你只要不断对自己重复一句话：“跟普通的数一样，只不过是逢2而不是逢10进1。
        
        2.3.1比特‌💄⌨🙄🤞
        
        表示数字信息的最基本单位是比特（bit)。英文bit是合并binary digit(二进制数字）之后造出来的，造这个词的人是统计学家约翰·图基，时间是1940年代中期。（图基还在1958年发明了单词software——软件。）据说，鼎鼎大名的氢弹之父爱德华·泰勒更喜欢“bigit”这个词，但这个词最终没有流行起来，真是谢天谢地。binary是指只有两个值的东西（前缀“bi”的意思就是“两个”），事实也的确如此：一个比特就是要么是0要么是1的一个数，没有其他可能。而十进制中有0到9,共有10种可能的值。
        
        只用一个比特，可以表示任何二选一的事物。这种二选一的例子比比皆是：开/关、真/假、是/否、高/低、进/出、上/下、左/右、南/北、东洒、男/女，等等。

👨‍⚕️‍🧢🔭😷🙌

        一个比特足以让人确定选择了两个中的哪一个。举个例子，我们可以用0表示“关”，用1表示“开”，或者反过来，哪个值表示哪个状态都无所谓，只要大家都没有意见就行。这张图是我的打印机的电源开关，由此可见，惯例还是用0表示“关”，用1表示“开”。


        一个比特表示开/关、真/假之类的二选一的情形没有问题，但我们经常还要面对更多选项，表示更复杂的事物。为此，可以使用一组比特，然后为不同的0和1的组合赋予不同的含义。比如，可以用两个比特来表示大学四年：新生（00)、大二（01)、大三（10)和毕业班（11)。如果再多考虑一种情况，比如研究生，那两个比特就不够用了，因为两个比特只有4种组合，没有第五种可能。但是三个比特没问题，实际上三个比特能表示8种不同的情况，这样我们就可以把教师、教工和博士后都包含进来。三个比特的全部组合为：000、001、010、011、100、101、110和111。
        👨‍🎨‌🧦📱🥱🤝
        比特数与它们所能表示的情况数之间有一个关系，很简单:N个比特能表示2^N种组合，即2x2x2x…x2(乘N次)。据此，就有：


        对于十进制数呢？其实也有类似的关系：N个十进制数字，可以表示10^N种不同的情况（我们称为“数值”）：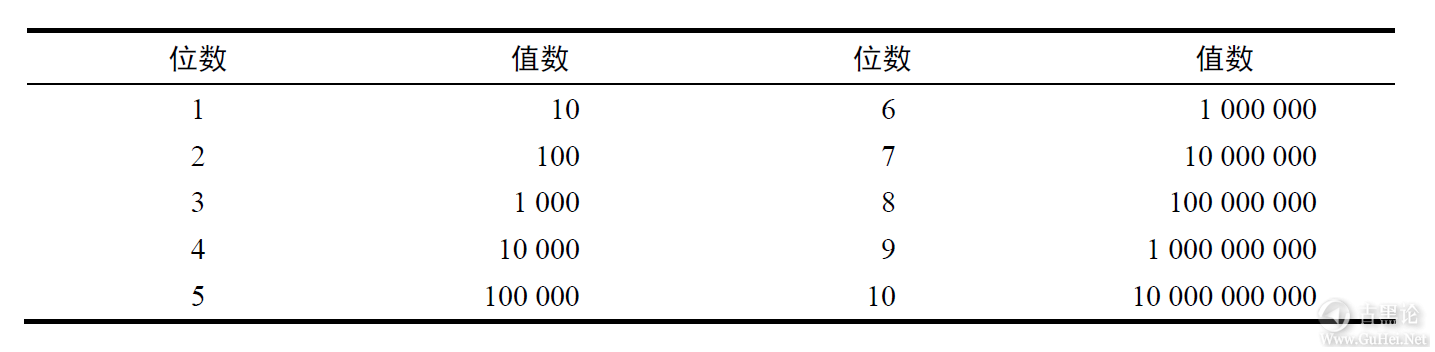

🤙🗽🍏♑🪰‌
       2.3.2 2的幂和10的幂
        
        由于计算机中的一切都是以二进制形式来处理，因此像大小、容量等概念一般都是用2的几次幂来表达的。如果有N比特，那么就有2^N种可能的值，所以知道2的幂是多少（比如到2^10)是很有用的。但随着数值越来越大，完全记住它们也没有什么必要。好在有一种简便的方法，可以得到它们的近似值：2的某次幂与10的某次幂接近，它们的对应关系严格有序，容易记忆：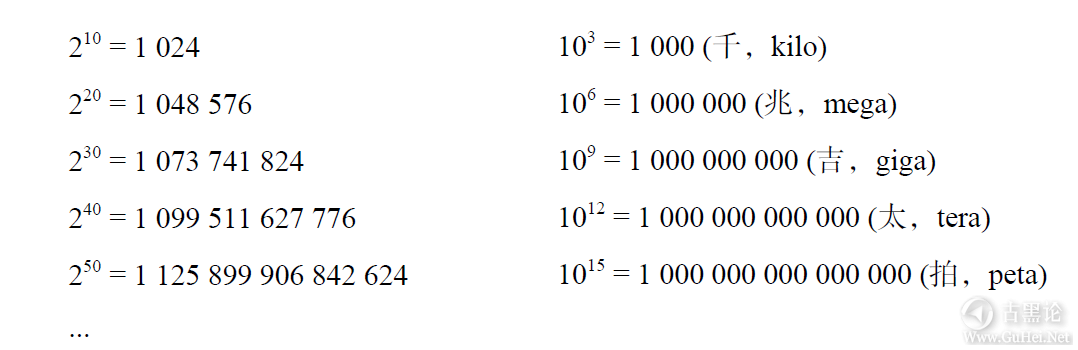

👈🚤🍽🚭🦟‍
        随着数值增长，这个近似值的误差也会增大，不过到了10^15这么大的时候误差也就12.6%，所以还是可以在很大范围内使用的。经常会有人混淆上述2的幂与10的幂之间的关系（有时候是想用来支持他们的观点），于是kilo或1K可能是指1000，但也可能指210即1024。一般来说，这种混淆导致的误差并不大，因此在涉及很大的比特数时，用2和10的幂来做心算没什么问题。
        
        说起来可能有点不值当的，但这种差异有时候也会带来麻烦。例如，著名硬盘驱动器制造商美国希捷公司，就曾因为这种差异在加州卷人一场集体诉讼。“原告称希捷公司对存储容量的术语gigabyte(或GB)，使用的是十进制定义，即1GB=10^9(1000000000)字节，这是在误导消费者，因为计算机操作系统报告硬盘容量时，使用的是GB的二进制定义，即1GB=2^30。（1073741824)字节，相差大约7°%。”我个人并不认为很多消费者被严重误导了，但希捷公司选择了和解，并没有据理力争。
        🧓‍🦺💉😡👈
        2.3.3二进制数值
        
        如果每个数字都能按照通常的进位法则来解释，那么一系列比特就可以表示一个数值，只不过此时的基数是2,而不是10。0到9,共10位数字，足以为10个项目计数或分配标签。如果数量超过10,则必须使用更多位数字，比如两位十进制数字可以表示的数值或标签能达到100个，即00到99。多于100的时候，就要用三位数字，其表示的范围是1000,即000到999。（根据约定俗成的做法，我们平时不会写出数值前导的零，但这些零是暗含的。另外，我们平时计数也都从1而非0开始。）
        
        十进制数值实际上是10的某次幂之和的简写，比如1867就是1x10^3+8x10^2+6x10^1+7x10^0，即1x1000+8x100+6x10+7x1，即1000+800+6+7。上小学的时候，你把它们叫做个位、十位、百位……。这些概念我们太熟了，熟到根本不用去想。
✋⛵🥚🅿🪶‎        
        二进制数也一样，只不过基数是2,不是10,而且只涉及0和1两个数字。比如可以把二进制数11101看成1x2^4+1x2^3+1x2^2+0x2^0+1x2^0。，用十进制来表示，就是16+8+4+0+1，即29。
        
        既然比特序列可以解释为数值，那么自然就有了为项目分配二进制标签的模式：按数值顺序排列。前面我们看到了为新生、大二、大三、大四学生分配的标签00、01、10、11，它们分别是十进制数值的0、1、2、3。紧接着的序列是000、001、011、100、101、110、111，也就是十进制数值0到7。
        

👨🦱‍🥼💿😫

        下面我们做个练习，看你理解了多少。我们都熟悉扳着自己的手指从一数到十，要是你用二进制数来数（每个手指，包括大拇指，都代表一位二进制数)，最大能数到多少？值的范围有多大？如果你数到132,发现它的二进制表示是一个似曾相识的手势，那说明我前面讲的你都理解了。
        
        前面我们都看到了，把十进制转换成二进制很容易：只要把相应位置上值为1的2的对应次幂加起来即可。而把十进制转换成二进制要难一些，但也不太难。就是反复地用2除十进制数。每次除完，把余数写下来，要么是0,要么是1，然后再用2除商。这样反复除下去，直到原来的数被除到等于0。最后得到的余数的序列，就是相应的二进制数，但顺序相反，所以要倒转一次。
        
        举个例子，把1867转换为二进制数的步骤如下：
🤝🚘🍪☪🐋‌

        反向读取这些位，能得到11101001011，把相应位上为1的2的对应次幂加起来可以验算：1024+512+256+64+8+2+1=1867。
        
        整个过程的每一步都会产生剩余数值的最低有效位（即最右边的位)。其实，把一个很大秒数表示的时间转换成日、时、分、秒的过程与此类似：除以60得到分钟（余数是秒），结果除以60得到小时（余数是分钟），结果再除以24得到天数（余数是小时)。区别在于时间转换使用了不止一个基数，而是先后用到了60和24。

🖐🗺🍖➡🐠‏

        
        二进制的算术实在太简单了。因为总共才两个数字，加法和乘法表都只有两行两列。


        虽然你将来不太可能自己动手做二进制算术，但这两个如此简单的表，其实也说明了为什么相对于十进制算术，执行这种计算的计算机电路要简单得多。🧑‍🌾‏👠💊😛
        
        2.3.4字节
        
        在所有现代计算机中，数据处理及内存组织的基本单位都是8个比特。8比特被称为1字节，而字节（byte)这个词是由IBM的计算机设计师维尔纳·巴克霍尔兹（Wemer Buchholz)在1956年发明的。一个字节可以编码256个不同的值（2^8，即8个0和1的所有不同组合)，这个值可以是一个0到255间的整数，也可以是ASCII字符集中的一个字符，或者其他什么。
🧑‍🌾‌🧢💊🤬👂
        通常，为了表示更大或更复杂的数据，需要用到多个字节的字节组。两个字节有16比特，也就是16位，可以表示0到216-1(65535)之间的数值。两个字节也可以表示Unicode字符集中的一个字符，比如以下字符中的任意一个：

        
        这是两个字符，即“东京”，每个字符占两个字节。四个字节是32位，既可以表示“东京”，也可以表示最大直至232-1的值，这个最大值大约是43亿。用一组字节表示什么都可以，但CPU自己特别定义了一些适中的字节组（比如表示不同大小的整数)，以及处理这些字节组的指令。
        🧑‍💻‏🥼🧲😉👈
        要是你想把一或多个字节表示的数值写出来，那可以用十进制，如果它真是一个数值的话，十进制是最适合人类看的。如果你想看清每一个比特，特别是在不同比特编码不同信息的情况下，那还是二进制更方便。然而，二进制写起来太长了，比十进制格式长三倍还多，因此我们常用另一种替代数制，即十六进制。

        十六进制的基数是16,因此也就有16个数字（就像十进制有10个数字，二进制有2个数字一样），分别是0、1、...、9、A、B、C、D、E、F。每个十六进制数字表示4个比特，对于一般的数值，十六进制0相当于二进制0000,依此类推，十六进制9相当于二进制1001。接下去，十六进制A相当于二进制1010(十进制10)，十六进制B相当于二进制1011(十进制11)，依此类推，十六进制F相当于二进制1111(十进制15)。
        
        除非你是程序员，否则能看到十六进制数的机会并不多。一个例子就是网页中的颜色值。前面说过，计算机中一个像素的颜色值大都使用三个字节来表示，一个表示红色分量，一个表示绿色分量，最后一个表示蓝色分量，这就是所谓的RGB编码。‏👑📮😊🤳

        红绿蓝三个组分分别用一个字节表示，因此红色分量就有256种可能的值，三个组分中的绿色分量也有256种可能的值，同样，三个组分中的蓝色分量也有256种可能的值。于是一个像素可能的颜色值就是256x256x256种，听起来好多啊。我们可以用2和10的幂来简单估计一下这个数有多大。这个数是2^8x2^8x2^8,即2^24或2^4x2^20,大约是16x106,即1600万。在描述计算机显示器的情况下，你可能听说过这个数“超过1600万种颜色！）。
        
        一个深红色的像素可以表示为FF0000,换句话说，就是红色分量最多，没有绿色和蓝色；而一个鲜蓝色（并非深蓝色），即类似很多网页中链接的颜色，可以表示为0000CC。黄色是红加绿，因此FFFF00就是最深的黄色。阴影的灰色具有等量的红、绿、蓝组分，因此一个中等灰度的像素应该是808080,也就是红、绿、蓝组分的数量都相等。黑色和白色分别是000000和FFFFFF。
        🧑‍🌾‌🎩🔑🤮🙏
        Unicode编码表就使用十六进制来表示字符：


        上面两个字符的十六进制编码为67714EAC。第8章将会介绍以十六进制表示的以太网地址，第10章则会讨论用十六进制表示URL中的特殊字符。

✌🏝🎂➡🐂‍        有时候，在某计算机的广告中，我们会看到“64位”这个说法（“Windows7家庭高级版64位”）。什么意思呢？计算机在内部操作数据时，是以不同大小的块为单位的，这些块包含数值(32位和64位表示数值比较方便)和地址，而地址也就是信息在RAM中的位置。前面所说的64位，指就是地址。大约25年前，16位地址升级到了32位地址（足够访问4GB的RAM)，而现在32位又升级到64位。我不想预测什么时候会从64变成128,总得过上好一阵子吧，先不必想那么多。
        
        关于比特和字节，我们讨论到现在最重要的是必须知道，一组比特的含义取决于它们的上下文，光看这些比特看不出来。一个字节可以只用1个比特来表示男或女，另外7个空闲不用，也可以用来保存一个不大的整数，或者一个#之类的ASCII字符，它还可能是另一种书写系统中一个字符的一部分，或者用2、4或8个字节表示的一个大数的一部分，一张照片或一段音乐的一部分，甚至是供CPU执行的一条指令的一部分。
        
        事实上，一个程序的指令就是另一个程序的数据。从网上下载一个新程序，或者从CD-ROM或DVD中安装该程序时，它就是数据，所有比特将无一例外地被复制一遍。但在运行这个程序时，它的比特会被当成指令，CPU在处理这些比特时，又会把它们当成数据。
🖐🌡🥩✡🐯‎

        2.4小结
        
        为什么用二进制而不用十进制？因为制造只有两种状态（如开和关）的物理设备，比制造有十种状态的设备更容易。这种简单的性质在数不清的技术中都得到了利用，比如：电流（流动或不流动）、电压（高或低)、电荷（存在或不存在)、磁性（南或北)、光（亮或暗)、反射率（反光或不反光)。

👦‏👞🪗😄🙌

        约翰·冯·诺依曼很早就清楚地认识到了这一点，他在1946年说过：“我们储存器中最基本的单位自然是采用二进制系统，因为我们不打算度量电荷的不同级别。”
        
        为什么我们要知道或者要关心二进制数呢？这个问题问得好。至少在我的课上，理解另一种不熟悉的数制，相当于做了一次量化推理的练习，而有了这个训练之后，对我们习以为常的十进制的理解也将更深一层。除此之外，另一个意义在于，比特的数量在一定程度上揭示了涉及的空间、时间或者复杂性。再从根本上说，计算机值得我们花时间去理解，而二进制正是其运作的核心所在。
        👨🦱‎👑⌨😈🤞
        现实生活中也能找到一些与计算机无关的应用二进制的场景，或许是因为人们都认为大小、长短的加倍、减半是一种自然而然的运算。比如，高德纳在《计算机程序设计艺术》中描述了14世纪英国的酒器单位，分为13个二进制量级：2吉耳是1超品(chopin)，2超品是1品脱，2品脱是1夸脱，依此类推，直到2百瑞尔（barrel)是1豪格海（hogshead)，2豪格海是1派普（pipe)，2派普是1坦恩（tun)。
        这些单位中差不多还有一半仍然在英制液体度量体系中使用。当然，其中一些很令人陶醉的词，比如费尔金（firkin)和基尔德坎（kilderki)(2费尔金是1百瑞尔），今天已经很难得见了。