编码的奥秘8_其他进位制记数法

　　10对我们来说是一个非常重要的数字。10是我们大多数人拥有的手指或脚趾的数目，我们当然希望所有人的手指脚趾都是10个。因为我们的手非常适合数数，因而我们人类已经适应了以10为基础的数字系统：

👃🗽©🐤‎

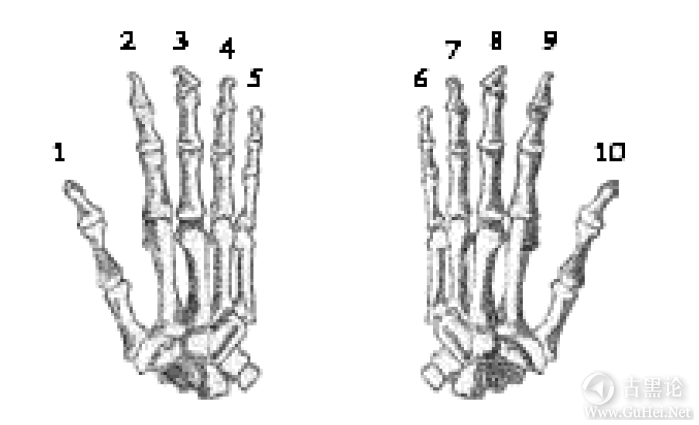
　　前面数章已经提到过，通常使用的数字系统称为以10为基础的数字系统或十进制。这个数字系统对我们来说非常自然，因而我们很难想像出还有其他的数字系统。事实上，当我们看到数字10的时候，不由自主地就会认为这个数是指下面这么多只鸭子：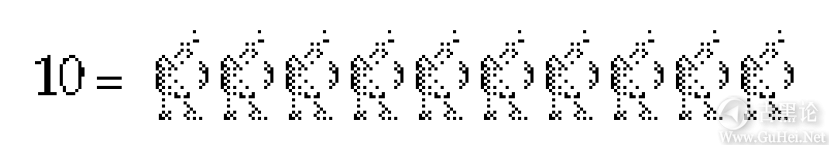


　　但是，数字10是指这么多只鸭子的唯一理由是因为这么多只鸭子与我们的手指数目相同。如果人类不是有那么多只手指，我们数数的方式就会有所不同，数字10就可能代表别的东西了。同样是数字10，可以指这么多只鸭子：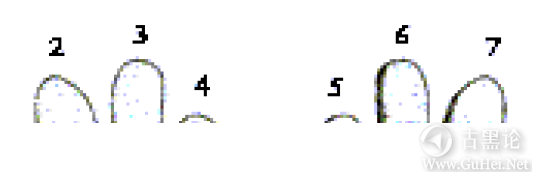

🦷🏠🍧♑🐉‎


　　或这么多只鸭子：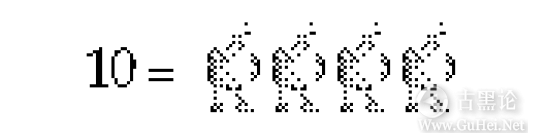
👵‎🕶📞😒🤳

　　甚至可以是这么多只鸭子：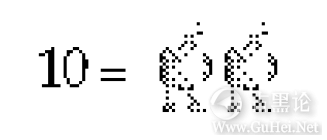


　　当我们明白了10可以指只有两只鸭子的时候，也就可以解释开关、电线、灯泡、继电器（或干脆就叫计算机）是怎样表示数字的了。
👎🗼🧊🅰‎


　　如果人类像卡通人物那样，每只手上只有4个手指会怎样呢？我们可能永远都不会想到要发明一种以10为基础的数字系统的问题，取而代之的是我们可能会认为数字系统基于8是正常、自然、合理、必然的，是毫无疑问的，是非常合适的。这时，就不能称之为十进制了，得将它称作为以8为基础的数字系统或八进制。

🖕🗺🍇⚛🐯‎
　　如果数字系统是以8为基础组织起来的，就不需要这样的一个符号：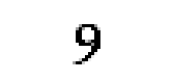

　　把这个符号拿给任何一个卡通人物看，都会有同样的反应：“那是什么？它是干什么用的？”如果再仔细想一会儿的话，你会发现连这样的一个字符也不需要：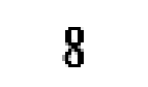

🧠⛪🌰®🐙‍　　在十进制数字系统中，没有专门用来表示10的符号，所在在八进制数字系统中，也没有专门用来表示10的符号。

　　在十进制数字系统中数数的方式是0、1、2、3、4、5、6、7、8、9，然后是10。在八进制数字系统中数数的方式是0、1、2、3、4、5、6、7，然后是什么呢？我们已经没有符号可用了，唯一的一个有意义的可用符号是10，的确是那样。在八进制数中，7之后紧接着的数字是10，但是10并不是指人类的手指那么多的数目。在八进制数中，10指的是卡通人物手指的数目：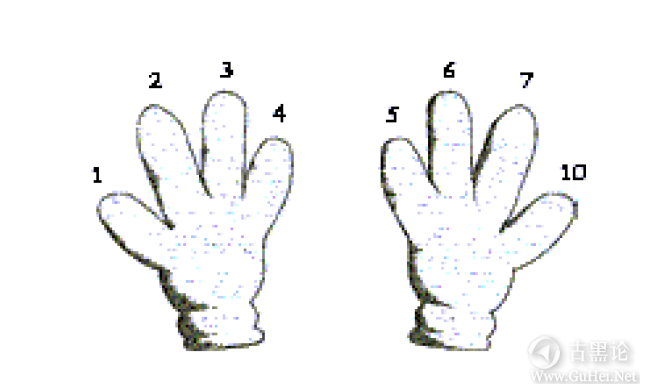


👎🏫🍏®🐤‏
　　继续数脚趾头：

　　使用非十进制的数字系统时，将数字“10”读作“么零”可以避免一些混淆。同样，“13”可以读作“么三”，“20”可以读作“二零”。要想真正避免混淆，可以将“20”读作“八进制二零”或“基于8的数二零”。

👍🚤🍌🈷🐖‌　　即使没有手指和脚趾帮忙，我们仍能够将八进制数继续数下去。除了要跳过那些含有8或9的数字以外，它基本上和数十进制的数是一样的。当然，相同的数字代表的数量是不同的：


　　最后一个数字读作“么零零”，是卡通人物拥有的手指数自乘的结果（即平方）。
🧓‌🥼⚔🤡👁

　　在写十进制或八进制数时，为避免混淆，可以借助使用特定的标记以区别表示数字系统。

　　下面用标记“TEN”表示十进制数，标记“EIGHT”表示八进制数。
👮‍♂️‌🩳🖲😡🤛

　注意，在上面一系列的八进制数中，有一些好整数，像100EIGHT、200EIGHT、400EIGHT。好整
数通常是指结尾有一些零的数。在结尾处有两个零的十进制数意味着它是100TEN即10TEN乘以10TEN；在八进制数中，结尾处有两个零表示它是100EIGHT即10EIGHT乘以10EIGHT（或8TEN乘以8TEN，等于64TEN）。

🧑‍🚀‌🧢📱🤑👌
　　你可能已经注意到了，好的八进制整数100EIGHT、200EIGHT和400EIGHT与十进制数64TEN128TEN、256TEN相等，它们都是2的整数次幂。例如，400EIGHT等于4EIGHT乘以10EIGHT乘以10EIGHT，所有这些数都是2的整数次幂。任何时候，将2的整数次幂和另一个2的整数次幂相乘，得到的仍是2的整数次幂。


　　下表给出了一些2的整数次幂的十进制及其对应的八进制的表示形式：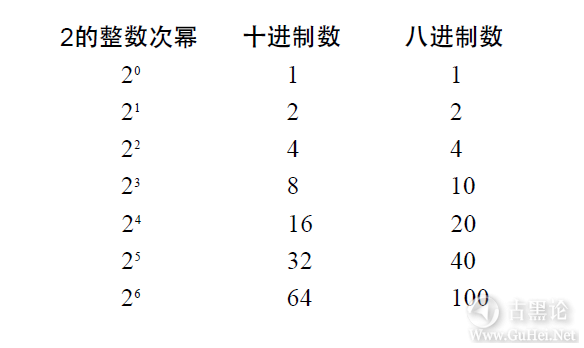
👦‌👙⌨🥱🤟

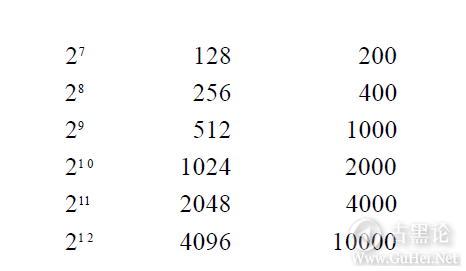
　　最右边一列的好整数给我们一个暗示：十进制以外的数字系统可能对使用二元码有所帮助。

　　八进制数字系统和十进制数字系统在结构上没有什么差别，只是在细节上有一些差异。例如，八进制数的每一个位置代表的值是该位数字乘以8的整数次幂的结果：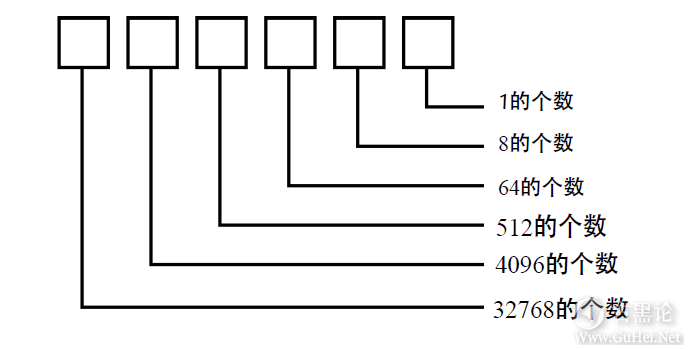

👃🚘🍍®🐢‍

　　这样，八进制数3725EIGHT可以拆分成这样：

　　3725EIGHT=3000EIGHT+700EIGHT+20EIGHT+5EIGHT

✌🌦🍟✔🐯‏　　还可以写成另外几种不同的形式。下面就是其中的一种，采用十进制形式的8的整数次幂：


　　采用八进制形式的8的整数次幂的情况：

👎🔥☪🦕‎

　　还有另外的一种拆分形式：


　　如果算出其十进制的结果，会得到2005TEN。这就是将八进制数转换成十进制数的方法。

👍🍍🆘🐶‏
　　可以采用与做十进制加法和乘法相同的办法来做八进制数的加法和乘法。唯一真正的区别在于要采用不同的表格来对各个数字进行乘法或加法运算。下面是八进制数的加法表：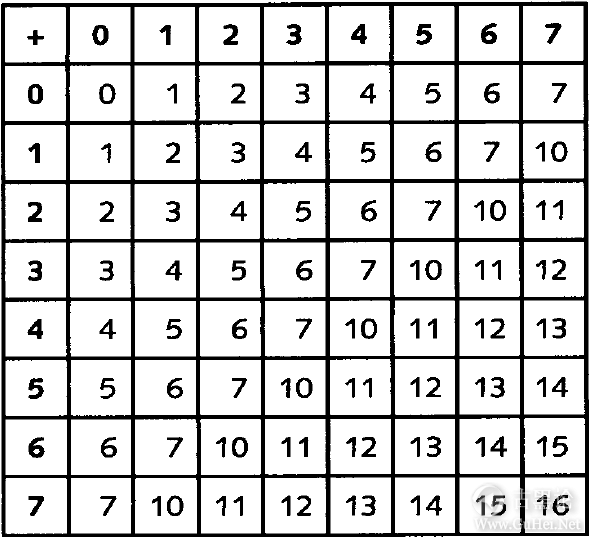


　　例如，5EIGHT+7EIGHT=14EIGHT。可以采用与做十进制加法相同的方法将两个稍长一点儿的八进制数相加：
✍🌡🍧ℹ🐮‌　　先从最右边的一列做起，5加上3等于10，该位写下0，向前进1；1加3加4等于10,该位写下0，向前进1；1加1加6等于10。


　　同样，在八进制中，2乘以2仍然等于4。但是3乘以3却不等于9，那是多少呢？3乘以3等于11EIGHT，此数与9TEN所代表的数量相等。下图是完整的八进制数的乘法表：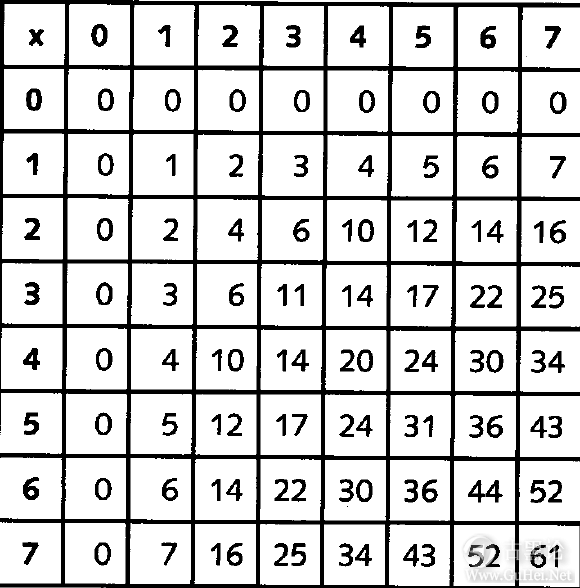
🧑‍💻‍🦺🧬🙃👁


　　这里，4×6等于30EIGHT，也即表明30EIGHT和4×6的十进制结果24TEN是等值的。

　　八进制数字系统与十进制数字系统一样，都是有效的，但八进制数字系统在理解上更深了一层。既然我们已为卡通人物开发出了一套数字系统，就再给龙虾开发一套适合它们用的数字系统吧。龙虾根本没有手指，但它两只前爪的末端都有螯。适合于龙虾的数字系统是四进制数字系统或称为基于4的数字系统：
💅🦼🍪⁉🐉‏

　　四进制数可以这样来数：

　　0、1、2、3、10、11、12、13、20、21、22、23、30、31、32、33、100、101、102、103、110，等等。

👩‍👒🛋🤤👀

　　这里不打算在四进制数上花太多的时间，因为还有更重要的事情要做。但我们还是要看
一下四进制中的每一位是怎样和4的某个整数次幂相对应的：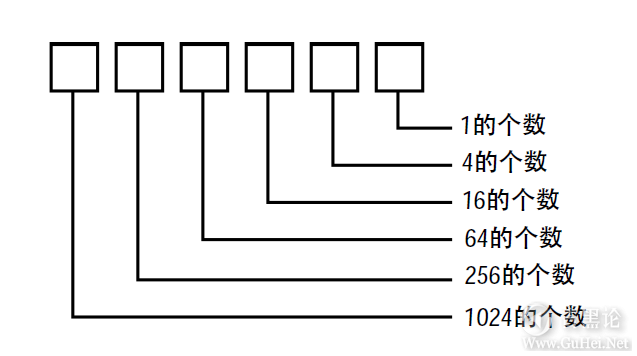

🦴🌡🥑🆘🦉‎

　　四进制数31232可以写成：


　　也可以写成：

‏🩳🔑☠🦴

　　还可以写成：


　　如果以十进制数的形式计算其结果，就会发现31232FOUR等于878TEN。

💪🌡🎂📵🐟‌

　　现在，我们要做一个跳跃并且是最远的一跳。假定我们是海豚，并且必须用两鳍来数数。则这个数字系统就是基于2的数字系统或二进制的。这样似乎只需要两个数字，即0和1。


🖕🏦🍏‼🦕‍　　现在，0和1已是你要处理的全部问题，需要练习一下才能习惯使用二进制数。二进制数最大的问题是数字用完得很快。例如，下图是海豚怎样用它的鳍数数的例子：



　　是的，在二进制中，1后面的数字是10。这是令人惊讶的，但也并不奇怪。无论使用哪种数字系统，当单个位的数字用完时，第一个两位数字都是10。在二进制系统中，可以这样来数数：
👂🥣☪🐉‏
0、1、10、11、100、101、110、111、1000、1001、1010、1011、1100、1101、1110、1111、10000、10001、⋯⋯

　　这些数看起来好像很大，实际上并不是这样。更准确地说二进制数长度增长的速度要快过二进制数增大的速度：
👳‍🦺✏😄🖐

　在多位二进制数中，数字的位置和2的整数次幂的对应关系为：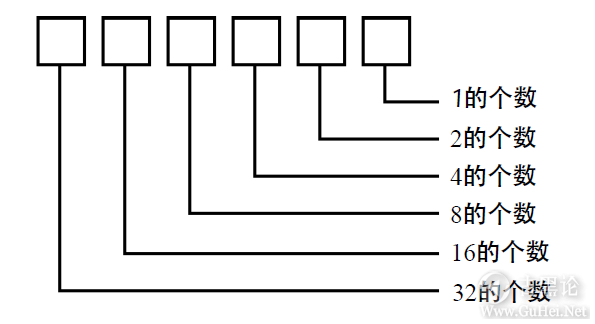


　　因此，任何时候由一个1后跟几个零构成的二进制数一定是2的整数次幂。2的幂与二进制数中零的个数相等。下面是扩充的2的各次幂的表，可用来说明这条规则：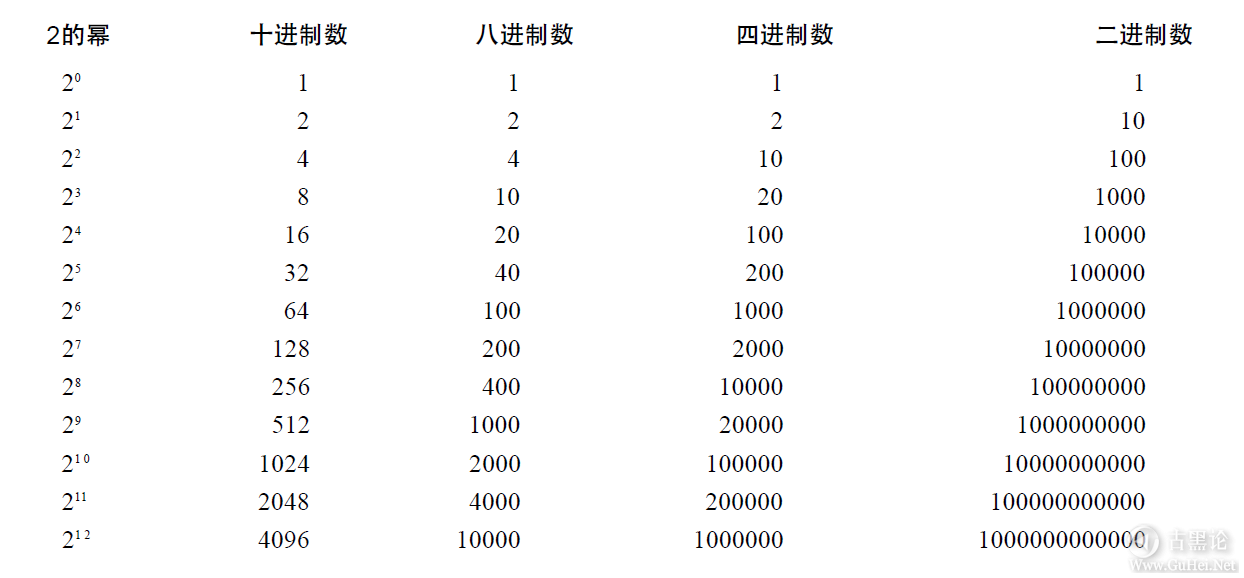

👴‍🩳📏🤮✌

　　假定有一个二进制数101101011010，它可以写成：

👦‌🥼🖌😄👍

　　也可以这样写：


　　如果将各个部分以十进制数的形式相加，得到2048+512+256+64+16+8+2＝2906TEN。

🤞🌞🫑🈸🦦‎　　将二进制数转换成十进制数非常简单，你可能更喜欢借助已准备好的模板进行转换：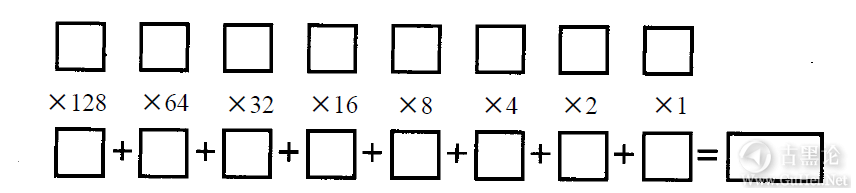


　　这个模板允许你转换最大长度为8的二进制数，但它扩充起来非常容易。使用时，将8个二进制数字放到上部的8个小盒子中，一个盒子放一个数字。做8个乘法运算，将结果分别放到底部的8个小盒子中。将8个盒子中的数字相加就得到最终结果。下面是将10010110转化成十进制数的例子：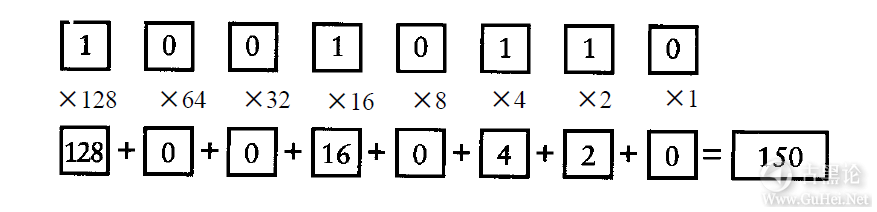

🤳🚂🥩🐮‏


　　将十进制数转换成二进制数就没那么直接了。但这里也有一个帮助你将0～225范围内的十进制数转换成二进制数的模板：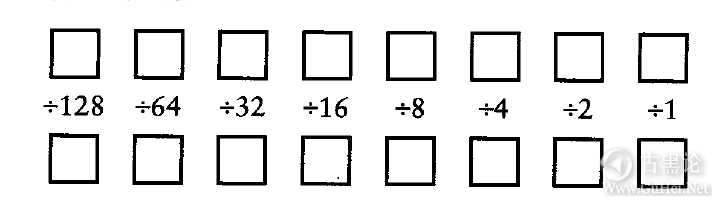
👩‍✈️‍🧢🪓😉🤞



　　实际转化过程要表面上看的麻烦得多，所以一定要仔细按照下面的指导来做。将整个十进制数（应小于等于225）放在左上角的方格中。用除数（128）去除那个数（被除数），如下图所示。将商写在正下方的盒子中（即左下角的盒子中），余数写在右边的盒子中（即上面一行左数第二个盒子中）。用第一个余数再除以下一个算子64。依照模板的顺序用同样的方法继续做下去。

👏🌕🥑⚛‍

　　记住，每次求得的商只能是0或者1。如果被除数小于除数，商为0，余数和被除数相等；如果被除数大于除数，商为1，余数为被除数与除数之差。下面是将150转换成二进制数的过程：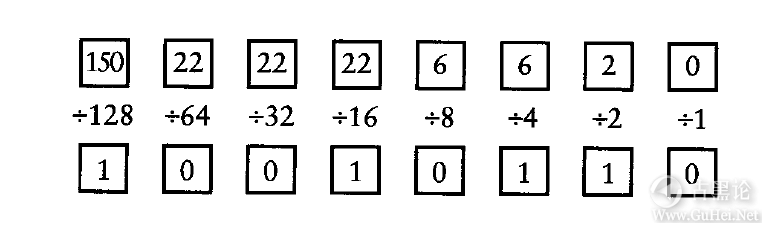


　　如果要做两个二进制数的加法或乘法，也许直接采用二进制来做比转化成十进制再做还要简单。这将是你真正喜欢二进制数的地方。如果只需记住下面的二进制加法表就可以做加法运算，也就不难想象掌握加法运算该有多快：
🧑‍⚕️‎👞🧯🙂👄

　　用二进制加法表将两个二进制数相加：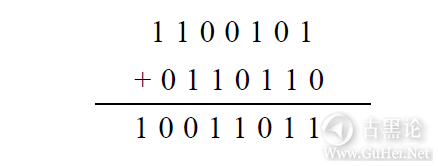


　　从最右边的一列开始做起：１加上０等于１；右数第2列：0加上1等于1；第3列：1加上1等于0，进位为1；第4列：1（进位值）加上0再加上0等于1；第5列：0加上1等于1；第6列：1加1等于0，进位为1；第7列：1（进位值）加上1再加上0等于10。
💅💈🥛➡🐥‌
　　乘法表比加法表更简单，因为该表可以由两个基本的乘法规则推导出来：零乘以任何数都等于0，1与任何数相乘仍是那个数本身：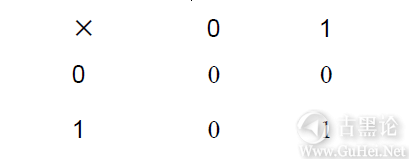

👌🌡🥭🐉‌

　　下面是13TEN与11TEN以二进制数的形式做乘法的过程：最后结果是143TEN。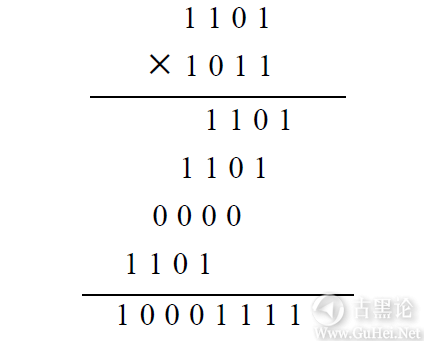




👃🚂🦞♾🦉‎

　　人们在使用二进制数的时候通常将它们写成带有前导零的形式（即第一个1的左边有零）。例如，0011而不写成11。这些零不会改变数字的值，只是起到一些装饰作用。例如，下面是二进制的前16个数以及和它们等值的十进制数：


👄🏫🍒🆚🐋‎　　让我们再仔细看看这些二进制数字。考虑一下这4个垂直列中每一列的0和1，注意它们在一列中自上而下是以怎样的规律变化的：


　这是很有规律的，难道不是吗？事实上，只要再重复这16个数字并且在每个数字的前面放一个1就可以很容易地写出后面的16个数字：


　　下面是看待这些数字的另一种方式：在数二进制数的时候，最右边的数字（也称最低位数字）是在0和1之间变化的。当它每次从1变到0时，右数第二位数字（也称次低位数字）也要发生变化，或者从0变到1，或者从1变到0。每次只要有一个二进制数位的值由1变到0，紧挨着的高位数字也会发生变化，要么从0变到1，要么从1变到0。
👌🔥🥣❎🦮‍

　　我们在写十进制中比较大的数字时，通常每三个数字之间留一点儿空隙，这样，我们一看就知道这个数的大概数值。例如，当你看到数字12000000时，你可能不得不去数其中0的个数，但如果看到的是12000000，则马上就能知道是一亿两千万。二进制数的位长度增加得特别快。例如，一亿两千万的二进制表示为：


👊🌞🦀✡🐢‌101101110001101100000000


为了让它更易读，通常是每四个数字之间用连字符或空格来分开。例如；1011-0111-0001-1011-0000-0000或101101110001101100000000。后面会讲到更简单的二进制数的表示方法。

👦‍🕶📀🙂👎

　　通过将数字系统减少至只有0和1两个数字的二进制数字系统，我们已经在能够接受的范围内做了深入的讨论。不可能找到比二进制数字系统更简单的数字系统了。二进制数字系统架起了算术与电之间的桥梁。前面各章中，我们所看到的开关、电线、灯泡、继电器等物体都可以表示二进制数0和1：
🧑‍⚕️‌🦺🗑😷✌

　　二进制数与计算机密切相关！

　　大约在1948年，美国数学家John Wilder Tukey（生于1915年）提前认识到二进制数将在未来几年中随着计算机的流行而发挥更大的作用。他决定创造一个新的、更短的词来代替使用起来很不灵活的五音节词—binary digit。他曾经考虑用bigit或binit，但最后还是选用了短小、简单、精巧且非常可爱的单词bit(比特)来代替binary digit这个词。🧑‍⚕️‎💎💶😍👎